Новая школа 3

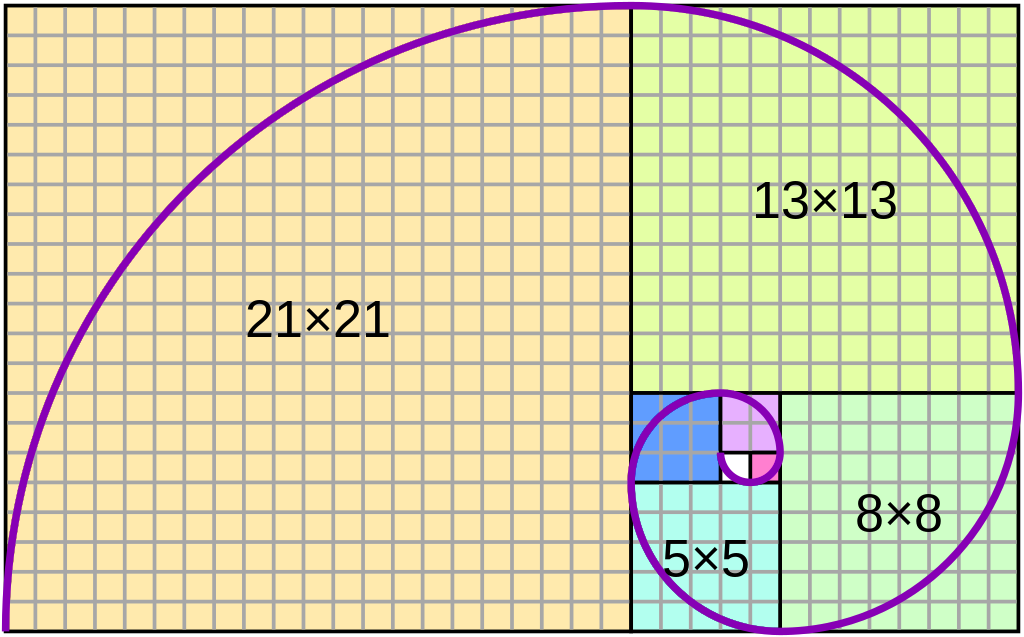
Числа Фибоначчи представляют собой последовательность чисел, в которой каждое последующее число является суммой двух предыдущих. Эта уникальная последовательность была введена в европейскую математику в XII веке итальянским математиком Леонардо Пизанским, более известным как Фибоначчи, хотя подобные последовательности были известны в индийской математике гораздо ранее. Числа Фибоначчи начинаются с 0 и 1, а каждое последующее число равно сумме двух предшествующих: 0, 1, 1, 2, 3, 5, 8, 13, 21 и так далее.

Свойства чисел Фибоначчи

Числа Фибоначчи обладают множеством интересных свойств и взаимосвязей, среди которых:

• Золотое сечение. Отношение последовательных чисел Фибоначчи стремится к константе золотого сечения (приблизительно 1,618), которая считается идеалом гармонии и пропорций в искусстве и архитектуре.
• Природные явления. Числа Фибоначчи находят отражение в природе: расположение листьев, ветвление деревьев, строение цветков и плодов, количество спиралей в шишках и ананасах часто соответствуют числам этой последовательности.
• Математические свойства. Сумма первых $n$ чисел Фибоначчи равна $(n+2)$-му числу минус 1. Кроме того, существуют формулы для нахождения чисел Фибоначчи, которые не требуют вычисления всех предыдущих чисел последовательности.

Приложения

• Теория чисел и криптография. Числа Фибоначчи и связанные с ними математические структуры находят применение в теории чисел, алгоритмах и криптографии.
• Компьютерные науки. Алгоритмы, использующие числа Фибоначчи, применяются в теории поиска и сортировки, а также в оптимизации и расчетах.
• Природные науки и биология. Изучение структур и процессов в природе, следующих закономерностям Фибоначчи, помогает глубже понять принципы организации живых систем.
• Искусство и архитектура. Золотое сечение, тесно связанное с числами Фибоначчи, на протяжении веков использовалось в искусстве и архитектуре для создания гармоничных и пропорционально совершенных произведений.